DFS와 BFS를 다뤄보고자 합니다. 여기서 DFS는 깊이 우선 탐색는 보통 재귀함수를 이용한 풀이가 주를 이루고, BFS는 너비 우선 탐색으로 큐를 이용한 풀이가 주를 이룹니다.

그림과 같이 dfs는 하나의 길을 우선적으로 파고 빠져나온 후 다음 경로로 이동하는 탐색방법입니다.
이와 다르게 bfs는 가장 가까운 노드부터 탐색합니다. 위 그림에서 보면 각 층별로 탐색하여 아래로 내려가는 구조일 것 입니다.
2. DFS
DFS에 대한 개념은 그렇게 어렵지 않지만 이를 문제에 적용하는 것은 상당히 어려웠습니다. 두 가지 풀이방법에 대해서 배웁니다.
재귀함수를 이용한 풀이 그리고 스택을 이용한 풀이입니다. 스택으로 이용한 풀이는 코드를 보고 이해하기 편했지만 재귀함수를 이용한 풀이는 직접 손으로 그려보지 않으면 이해하기가 어려웠고 더더욱 빈 에디터에 손수 코드를 작성하려면 막막하였습니다.
DFS가 코딩테스트에 자주 출제되는 주제인만큼 많은 연습이 필요할 것 같습니다.
다음은 DFS 풀이 예제입니다.
def dfs(graph, v, visited):
visited[v] = True
print(v, end=' ')
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visited = [False] * 9
dfs(graph, 1, visited)
3. BFS
BFS는 DFS에 비해 이해하기 쉬웠습니다. collectinos의 deque를 이용하면 쉽게 큐를 사용할 수 있습니다. 다음은 BFS 풀이 예제입니다.
from collections import deque
def bfs(graph, start, visited):
q = deque([start])
visited[start] = True
while q:
v = q.popleft()
print(v, end=' ')
for i in graph[v]:
if not visited[i]:
q.append(i)
visited[i] = True
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visited = [False] * 9
bfs(graph, 1, visited)
4. 트리
graph 와 tree의 차이점
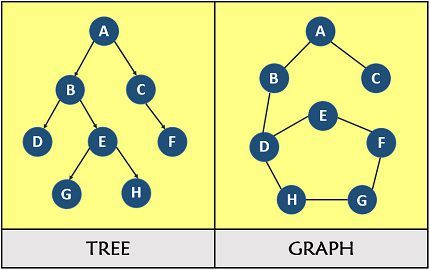
트리는 순환 구조를 갖지 않는 단방향 그래프라고 할 수 있습니다.
트리 중에서 이진트리란 모든 노드의 자식노드의 개수가 최대 두 개까지만 가지는 트리를 말합니다.
- 이진트리에서 자식노드가 없거나 한 개인 것도 상관없이 이진트리입니다!!
이진트리 중에서도 완전이진트리란 왼쪽부터 노드가 빠짐없이 채워져 있는 트리를 말합니다.
왼쪽부터 차례로 봤을 때 끝 노드는 없어도 되지만 중간에 노드가 빠진상태로 진행된 이진트리는 완전이진트리가 아닙니다
'부트캠프' 카테고리의 다른 글
| [22일차] TIL - Week3 Test (0) | 2022.03.31 |
|---|---|
| [19일차] TIL (Quick Sort) (0) | 2022.03.28 |
| [17일차] TIL - Heap (0) | 2022.03.25 |
| [16일차] TIL - Week2 Test (0) | 2022.03.24 |
| [13일차] TIL - Back Tracking (0) | 2022.03.21 |
![[알고리즘 2주차] WIL (Graph, DFS, BFS, Tree)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FPxOn7%2FbtrxwZnBBAj%2FwB6B0UnZELEyM7bzt4YXkk%2Fimg.png)